dziękuję
luked: rozwiąż nierówność x2+1/2x < 1
19 lis 21:17
lula: D: 2x≠0
x≠0 D=R/{0}
(x
2−2x+1)2x<0
Δ=4−4=0
x
1=1 x
2=0
19 lis 21:26
luked: Bardzo dziękuję. Już rozumiem dlaczego mi nie wychodziło − trzeba wymnożyć przez kwadrat
podstawy. Ale nie rozumiem dlaczego. Może mi to ktoś wytłumaczyć?
19 lis 21:29
lula:
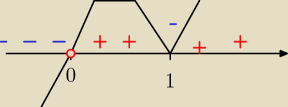
19 lis 21:32
roman: a czy mi może ktoś powiedzieć czy by można skrócić te 2x ze sobą ?
19 lis 21:33
roman: up
19 lis 21:35
luked: na to nawet ja ci mogę odpowiedzieć: nie możesz ich skrócić. Liczby możesz skracać tylko jeśli
u góry ułamka jest iloczyn (mnożenie) liczb i u dołu jest iloczyn (mnożenie) liczb. Tutaj masz
u góry: x2 +1−2x <−− czyli wyrazy luzem ze znakami. U dołu masz: 2x czyli tak naprawdę: 2x*1
(możesz to tak zapisać. Jest to iloczyn, ale niestety u góry nie masz iloczynu więc nie możesz
skrócić
19 lis 21:39
roman: Luked: look > thank Yu
but could i do like this
we have
Δ=3
so.... ?
19 lis 21:43
aa: no
19 lis 21:48
roman: to kto ma db bo raz Δ = 0 a raz 3
19 lis 21:51
aa: Δ=b2−4ac ax2+bx+c=0
19 lis 21:56
luked: nie prawda, w twoim przypadku też delta=0
zobacz:
x
2+1−2x < 0
19 lis 21:58
19 lis 21:59
luked: w takim przypadku 2x ci znika, dlatego trzeba pomnożyć przez (2x)2
19 lis 22:00
luked: nmzc
19 lis 22:00
roman: a nie powinno być tak :
x2−2x+1<0*2x
x2−2x+1<0
?
19 lis 22:02
roman: poczekaj nie odchodź jeszcze
19 lis 22:02
luked: | | x2+1−2x | |
no właśnie tak napisałem jak pomnożysz |
| * 2x To wyjdzie ci x2+1−2x. Natomiast 0 |
| | 2x | |
* 2x = 0
19 lis 22:04
aa: aby znak się nie zmienił to mnożysz przez mianownik do 2
19 lis 22:04
aa: wtedy masz pewność że mnożysz przez dodatnią liczbę
19 lis 22:06
19 lis 22:07
luked: dzięki aa
19 lis 22:10

